Background
This article was written in response to The Black Lamp’s appeal for new models to think about political organisation and action. This is a topic that I have been interested in for some time, and while I can only outline the sketch of a proposal here, I hope it will add to the debate. I will try to present my idea as simply as possible, assuming that readers do not have any technical background.
The classical political economists had an analysis of capitalism that relied on a very good general framework for thinking about complex dynamic systems like economies. We should think about using it for organisations too. Their framework was based on the idea that complex systems cyclically reconstitute or ‘reproduce’ themselves, perhaps at the same magnitude as before, or at a lower or higher level of activity[1]. Through consideration of the way in which the system reproduces itself on an ongoing basis, we obtain a good model of its most important attributes.
Much later, in the second half of the 20th century, the study of causality and feedback led to the beginnings of the discipline of cybernetics, and importantly for our purposes - management cybernetics. Stafford Beer’s famous Viable System Model (VSM) method for describing cybernetic systems was founded on a very similar principle. For him, the system was broken up into distinct essential functions, and the reconstitution of the system overall was said to be dependent on the adequacy of each of those functions[2].
The disciple of ‘viability theory’ further formalised this approach. For such complex systems, evolutions from one state (situation) to the next, deterministically or stochastically, required that the system maintains mechanisms to evolve its control functions in the presence of environmental challenges. As in cybernetics, it was understood that an ‘autopoietic’ (self organising - see box 1 for a glossary of terms used here) controller must be at work here[3], and in this article I will be focusing on one of the models which viability theorists have proposed for how this selection process works.
The purpose of this article is therefore to propose the bringing together of the framework of ‘reproduction’ of complex systems, along with the autopoietic controller method. This would be done for the purpose of understanding how a political organisation reconstitutes itself in the presence of environmental disturbances. A Markov Decision Process (MDP) is then used to demonstrate how this can be practically modelled.
By doing this, we can hopefully see more clearly how political organisations actually do make decisions in response to their self-perception of viability limits. This should not be confused with a model of what decisions the system should make. In order to think about that, we first need a model of the system as it actually exists - in Marxian terms, of the ‘simple reproduction’ of the system. The basis of the theory - the theory of ‘what the system actually does’ - is roughly that when the perception takes hold that the system cannot, for one reason or another, continue in the way which had made sense to them until this point, it modifies its functioning in a certain way.

Viability Theory
The following image and quotation are taken from the book ‘Viability Theory’.
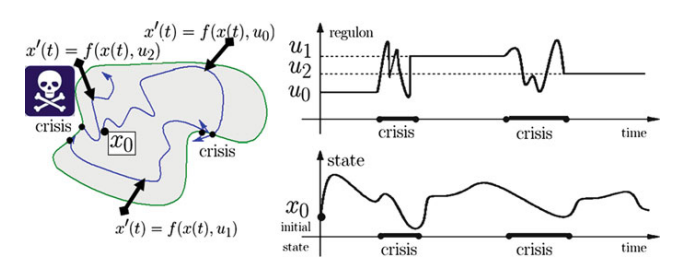
“Starting from x0 with the constant regulon u0, the solution evolves in K until time t1, (first punctuated equilibrium phase) when the state x(t1) is about to leave the environment K and when the constant regulon u0 must start to evolve. Then a critical phase happens during which velocities also evolve (as slowly as possible) to maintain viability, until time t1 when the control u1 := u(t1) can remain constant during a nonempty time interval: second punctuated equilibrium phase, after which a second critical phase” [3]
Viability theory thereby proposes that all viable systems have developed a given ‘path’ (we can consider it to be a ‘standard range of methods’) for successfully interacting with their environment, which is what allows them to exist as viable systems. I will be referring to this path as the ‘inertial trajectory’ of the system (above it is referred to as the "constant regulon"). Anyone who has been involved in any organisation will recognise this immediately - its the pattern of activities that the system settles into - which both makes sense to the specific organisation given its context and history, and is comfortably within its capabilities to carry out cyclically, thereby reproducing itself.
So let us note here that viability theory effectively presents us with two kinds of actions. Those of the inertial trajectory are the first, and the second are those which are above said to belong to the "critical phase", and which I will simply call ‘regulons’ - regulatory control actions. This is a new kind of action that is taken in order to maintain the viability of the system when it faces a certain (or probabilistic)[4] evolution into non-viability.
Real systems, it is posited, must develop these new methods in response to assessed viability threats - which thereafter become an element of their ‘standard range’ of methods (inertial trajectory). According to this specific theory of autopoietic actions, these new methods are chosen according to the following specific criteria. Firstly the regulon must be suitable to solve the assessed viability problem (perhaps up to a certain level of confidence)[4] and, on condition that this is true, the system must minimise the change to the system’s controls. The logical basis for this criteria is that small and slow changes to a social object’s standard methods are easier for the object to achieve than large and fast changes.
Viability theory thereby describes an ‘evolutionary’ control system, where attempted regulatory actions are 'chosen' with reference to the environment and the system’s self-understood capabilities, and not preselected by conscious controller design.
Starting point
Let’s assume therefore that we want to model an existing complex system - a political organisation. I propose that we need to describe the following:
- Firstly, the ‘state variables’ of the system - those variables which describe the system’s current situation. Following the method of classical political economy, these would show the ability of the organisation to reproduce itself in different respects. More precisely, I think we could frame these variables as the ‘logistical arrangements that the organisation has in place’ to build and retain its (i) support base, (ii) membership, and (iii) finances, among other aspects of reproduction.
Consider for example that the ‘current state’ in respect of ‘state variable (iii)’ describes the ability of the system to reconstitute itself in terms of the mechanisms by which it raises and retains finances.
- Secondly, the ‘action space’ of the system - the specific regulatory controls that the organisation might carry out, in order to positively impact on one or more of those logistical capabilities (while accounting for the reality that they may also have a negative impact on one or more other logistical capabilities).
- Thirdly, the starting ‘inertial trajectory’ of the system. This trajectory represents the evolution of the organisation’s states, assuming no additional actions are taken to modify it.
- Fourthly, the events which represent environmental disturbances that might negatively (or perhaps, in some senses, positively) affect the states of the system.
- Fifth, and perhaps most importantly - what does “viability” actually mean in the system’s self perception? To decide what ‘good’ or ‘bad’ capacity to reproduce this system actually means concretely, we must know the kind of characteristics that we associate here with viability, and those that we associate with non-viability.
Having done this, we need to consider some dynamics which arise from it all:
- We have seen that a viability theory methodology for autopoetic regulatory action selection requires a minimisation of the changes to the system’s controls, from among candidate actions that could be expected to solve the viability problem. I propose here that we frame this as ‘difficulty’ for the system (which can be considered analogous to ‘magnitude of control changes over time’).
We could therefore consider how difficult it is for the organisation to take different actions (assuming we do not care why an action is difficult, merely that it is). This ‘difficulty’ could for example take the form of an ideological discomfort in taking some kind of action in principle, or it could take the form of being ‘difficult’ to do in light of a lack of real resources. Furthermore, we can consider what impact the prior regulatory actions would have on these difficulty levels. For example, if the organisation has already improved its ‘financial reproduction capacity’, this may lower the difficulty level of regulatory actions which would incur a certain financial cost.
- We should also consider what impact the prior regulatory actions would have on the resilience of the system’s capacities, given environmental disruptions. For example, an organisation which has taken steps to improve its ‘membership building and retention arrangements’ can anticipate a heightened resilience in this respect, in the face of, for example, a ‘disruption’ like a hostile media campaign against the organisation.
In general, the impact of such environmental ‘events’ or ‘disruptions’ should be modelled as is usual in ‘robust control’ theory, not in terms of a stochastic range of magnitudes, but rather in terms of the maximum reasonably anticipated disruption.
Making choices:
Finally, arriving at what I actually want to propose: We can assume different scenarios, with given severities and frequencies of disturbances on different aspects of the system’s reproduction capacity. We then conservatively assume the impact of actions to counter the disturbances and improve the resilience of the system. The question which we would like to answer is then, ‘what actions appear to make the most sense to this organisation in different scenarios?’ (note that these may have little or no relation to what we imagine the ‘best’ possible actions to be).
By asking this question, and running some simulations, three things quickly become apparent. First, whether the state variables that we have selected make sense as they are, or whether we need new or different state variables to capture the system’s ability to reproduce itself. Secondly, what kinds of actions would likely be taken by the system, given different kinds of disruptions. Finally, which kinds of disruptions the system currently may not have any effective answer for.
As all of the parameters are user determined, we can establish any frequency or mix of inputs to the system that are useful. The output should be the ‘optimal policy’ given the method shown in the image below, and the inherent constraints which it implies for the simulation. This, let’s remember, is not a recommendation for what the system should do, but rather a model which optimises for what we think it would do to remain viable, based on all that we know about it.
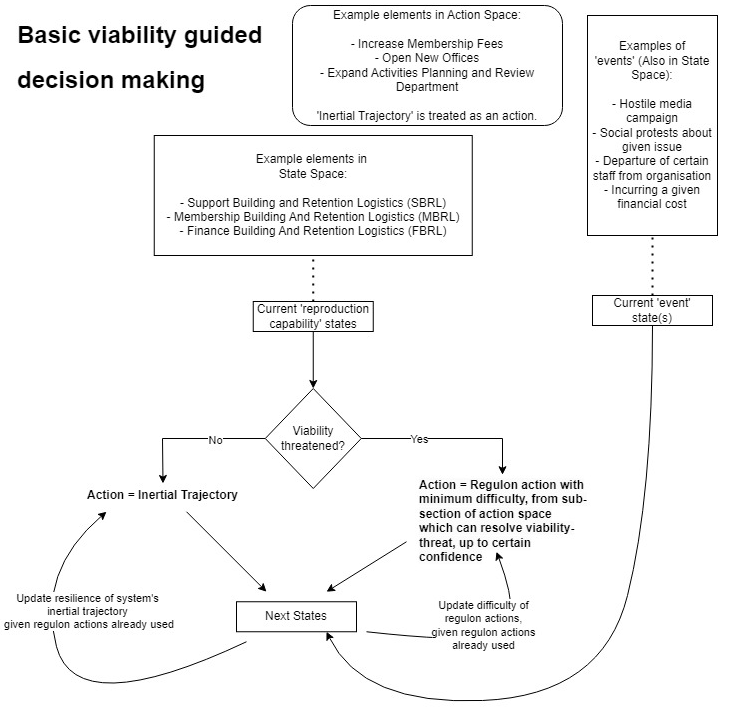
So let us quickly note the flow of events here. The ‘current states’ of logistical arrangements for reproduction give rise to the question of whether the systems’ viability is threatened. To be specific about this, we can divide all states in the system into viable and non-viable zones, and from that determine a ‘viability-threatened’ zone.
This informs the decision as to whether a ‘regulon’ action must be taken, or whether the system can continue on its inertial trajectory. In the former case, the regulon action is chosen in accordance with the viability theory method for autopoetic selection.
The next state is determined by the two-fold impacts of any ‘current events’, combined with the ‘selected action’. The result of this is a double feedback. In the first place by updating the resilience of the system’s inertial trajectory to future disruptions (reflecting the fact that this ‘regulon action’ has changed the ‘normal’ evolution of the system). In the second place, we update the difficulty for the system to choose various control actions in the future, which alters the autopoetic selection which will take place thereafter.
This latter point can be implemented in at least two ways - firstly by lowering appropriate actions’ difficulty levels, on condition that reproduction conditions are now present which make the action easier. Secondly, by increasing difficulty levels for actions that either have been taken already so that it won't be chosen again (as this action is already being cyclically deployed to reproduce our system, and it is not clear what the meaning choosing it again it would be), or which is ‘mutually exclusive’ with an action that has already been chosen.
In the next time step, the next ‘reproduction capability states’ take the place of their ‘current’ counterparts, while a new ‘event’ is probabilistically generated, and the process repeats.
Example simulation
Without going into the technical details of how a Markov Decision Process can be written and ‘solved’, let’s examine the above process to see some results I got for a toy model in the Gif image below.
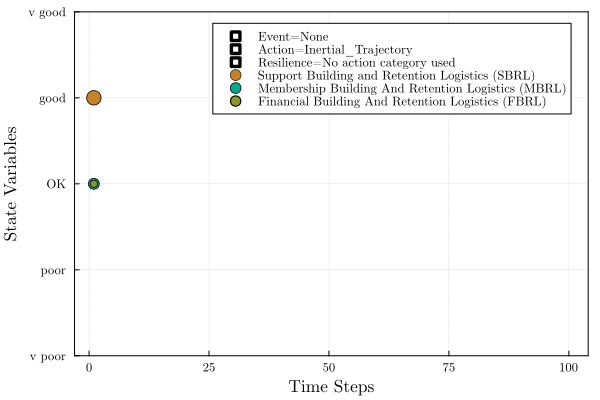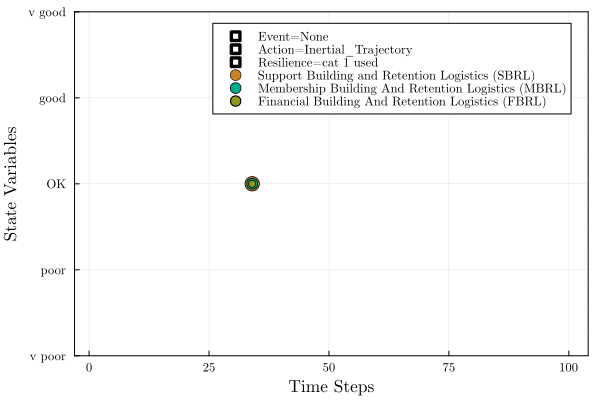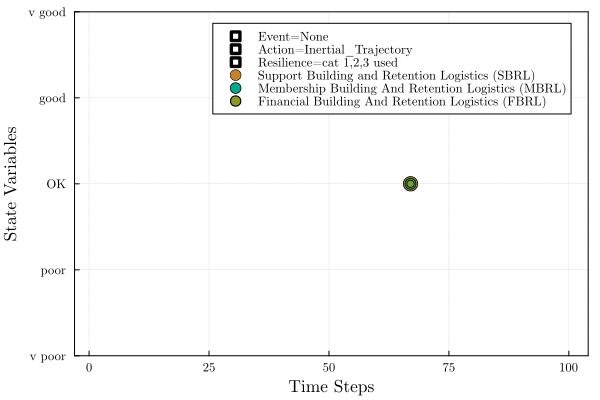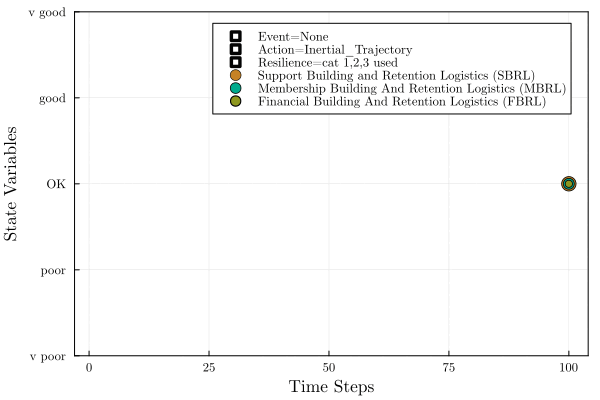
Firstly, to explain the current state of the ‘state variables’ on the Y axis of this plot, we can see a range from ‘very poor’ to ‘very good’. What do these terms mean? Again, that is something that would need to be specified for the particular organisation and how it understands ‘viability’. For now, let’s assume that this is all known, and that “very poor” represents non-viability (and the termination of the simulation, if any of our state variables was in this zone). Meanwhile “poor” represents the “viability-threatened” zone, which represents the area from which there is a given non-zero probability of transitioning into the “non-viable” zone. The other regions (OK, good and very good) can all be considered “viable” for this simulation, from where the state variables have a zero or very small probability of transitioning directly into the ‘non-viable’ zone.
We can see in the panel in the top right corner of the image that an ‘event’ can happen, which is a disruption of some kind. We can see that an action will be taken on each time step (which is either the ‘Inertial Trajectory’ or a regulatory action of some kind. Beneath this is a ‘resilience’ level, which indicates which categories of regulatory actions have been taken already during the simulation, and hence the kind of reinforcement that have been added to the system’s ability to suppress new disruptions.
Finally we have the state variables themselves - the system’s ability to reproduce its (i) popular support, (ii) membership and (iii) finances.
Because there appears at first glance to be a lot going on here, let me explain what happens in this particular simulation.
We begin with ‘good’ support building and retaining logistical arrangements, and ‘OK’ membership and financial building and retaining logistical arrangements. We then experience a disruption (“resignations from crisis management team”). This causes both the ‘support’ and ‘membership’ variables to drop to ‘poor’, from ‘good’ and ‘OK’ respectively. The regulatory action that is then taken is the easiest one which can move us from ‘poor’ to ‘OK’. This happens to be to ‘expand volunteering programmes’ (perhaps in order to free up personnel to replace those who have resigned). This brings the ‘support’ and ‘membership’ variables back to the ‘OK’ level.
The ‘inertial trajectory’ of the system has now been modified, as shown in the ‘resilience’ indicator, to incorporate the fact that the system has now included this regulatory action, and can consider it a mechanism which it now has experience with and can use, which it had not previously regarded as a normal part of its reproduction.
Some time-steps later, we have the series of events shown in the images below.
We next get hit by a “resignations from the public relations team” event, causing those same two state variables (membership and support reproduction) to again drop to ‘poor’. On this occasion, the chosen action is to “expand targeted recruitment advertising”, which has now become the easiest regulatory action that we expect to be effective.
In the second panel, we can see that this succeeds in raising the intended state variables from ‘poor’ to ‘OK’, but has the side-effect of lowering our systems’ “financial building and retention logistics’ variable to ‘poor’ (because “targeted recruitment advertising”, as a method to help reproduce the organisation, carries a recurring financial cost).
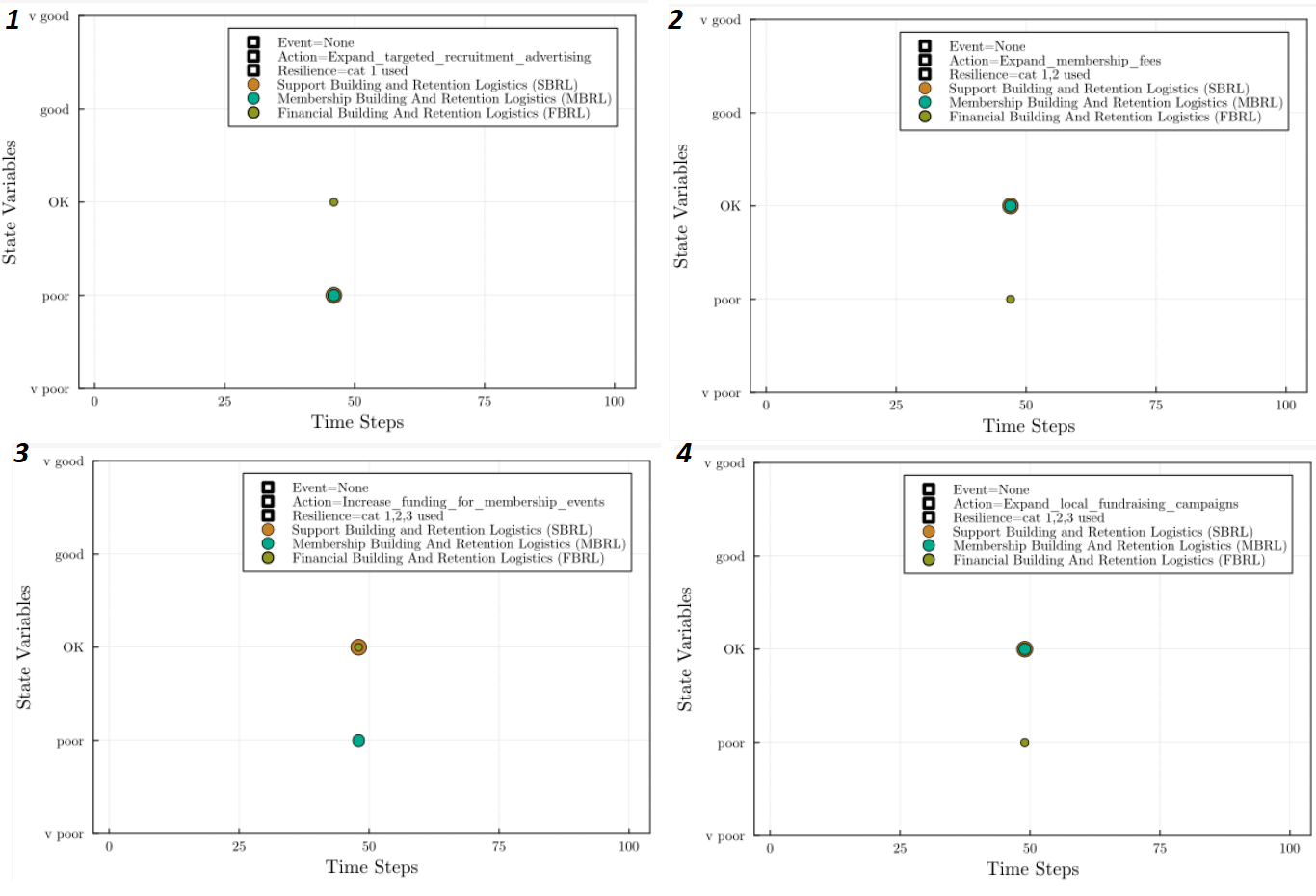
In the second panel, an additional action is thus taken to “expand membership fee”. This financial cost is thereby passed on to the organisation’s membership, returning the financial reproduction situation back to ‘OK’ in the third panel, where the ‘support building and retention’ variable also remains, unaffected by the expansion of the membership fee. The ‘membership building and retention’ has however taken a hit because of the increased membership fee.
In the third and fourth panels, this is passed back and forth again by new actions, to “increase funding for membership events”, to try to retain members, while “expanding local fundraising campaigns” to shore up the financial reproduction of the system given those new expenses.
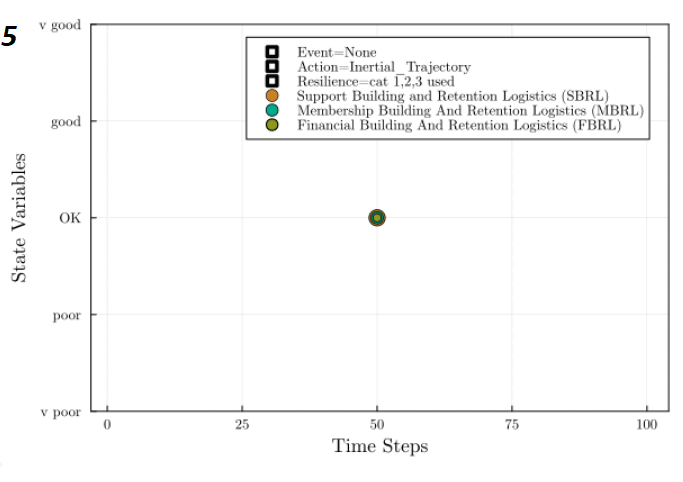
Finally in the fifth panel, we can see that the system has returned to its ‘inertial trajectory’, with no states currently in the ‘viability-threatened’ (or “poor”) zone. However, the inertial trajectory now includes additional ‘resilience’ to future disruptions in all three of the state variable categories, because of the regulatory actions that it has taken. Later events in this simulation did not cause the need for additional actions to be taken as a result of this improved resilience to disruptions.
Final thoughts..
Of course, the example that I’ve shown is very simple, with only a few actions, states and disruptions, and only very simple dynamics. But this is only a few days’ work. Much more is possible. For example, I think it’s clear that this model would benefit from temporal dynamics (e.g. how many time steps does an action require in order to take effect? For how long can it be expected to effectively work?). This would make the ‘time steps’ meaningful, and could be presented as ‘weeks’ or ‘months’. A real model would also likely have sublayers of Markov Decision Processes, expressing the system states and dynamics at fine levels of detail, and feeding them upwards to the overall system model. Hopefully you have already thought of a few other good additions while reading this.
This is the general method that I propose to use in order to think about these issues. We could further consider using reinforcement learning and other methods to model industrial disputes, social movements, housing occupations and so on. The advantage of using modelling is not only as a way to rethink our positive actions, but just as importantly, to rule out courses of action that we cannot stand over as probably effective. Doing so also forces us to directly confront and explicitly explain what we mean by ‘viability’ - what situation do we actually consider to be viable, and why.
In this article we have only been trying to better understand the system - to make a model. But by deepening our understanding of the system’s functioning, we can more clearly think about what steps could now proactively be taken, in order that the system’s viability is not threatened in the first place by disruptions. In other words, we place ourselves as the ‘controller’ on top of this autopoetic control system that we have looked at - resulting in a plan of action.
How would this be done? That will need to be the subject of future work. I think we can proceed in a way which flows from the model that we have seen already, thereby maintaining the dynamics that we believe to define this specific viable system. We can simply modify what we understand by ‘viability' for this system to be more ambitious - in Marxian terms, ‘reproducing of the system at a higher level’. Those characteristics which we previously designated as 'OK' for example would now be regarded as 'poor'.
We would find that new regulon actions would now be needed to achieve this, which must be consistent with the system’s self-perception of ‘difficulty’. We would be interested in doing this either to reinforce the existing system against potential problems, or to consider its future expansion. To reach this new level of viability means to take actions which reinforce the system’s ability to reproduce itself in all necessary respects at this level, along with its resilience to disturbances which might threaten its viability.
Works cited
[1] Capital, Karl Marx, Volume II, chapter 20, 515-516, Penguin 1992
[2] Brain of the Firm, Stafford Beer, Chapter 9 ‘Automatic Management’, 1972
[3] Viability Theory, New Directions, Second Edition (Aubin, Bayern & Saint-Pierre), Springer 2011
[4] Extending the viability theory framework of resilience to uncertain dynamics, and application to lake eutrophication (Rougé, Mathias & Deffuant), 2021
Donal Costello is a Masters degree student in Engineering Cybernetics at Kazan National Research Technical University named after A.N. Tupolev.



.png)


